线性代数中最被低估的真相:矩阵就是图,图就是矩阵。
把矩阵看成图,是破解复杂结构的“作弊码”,让难题变得直观易懂。
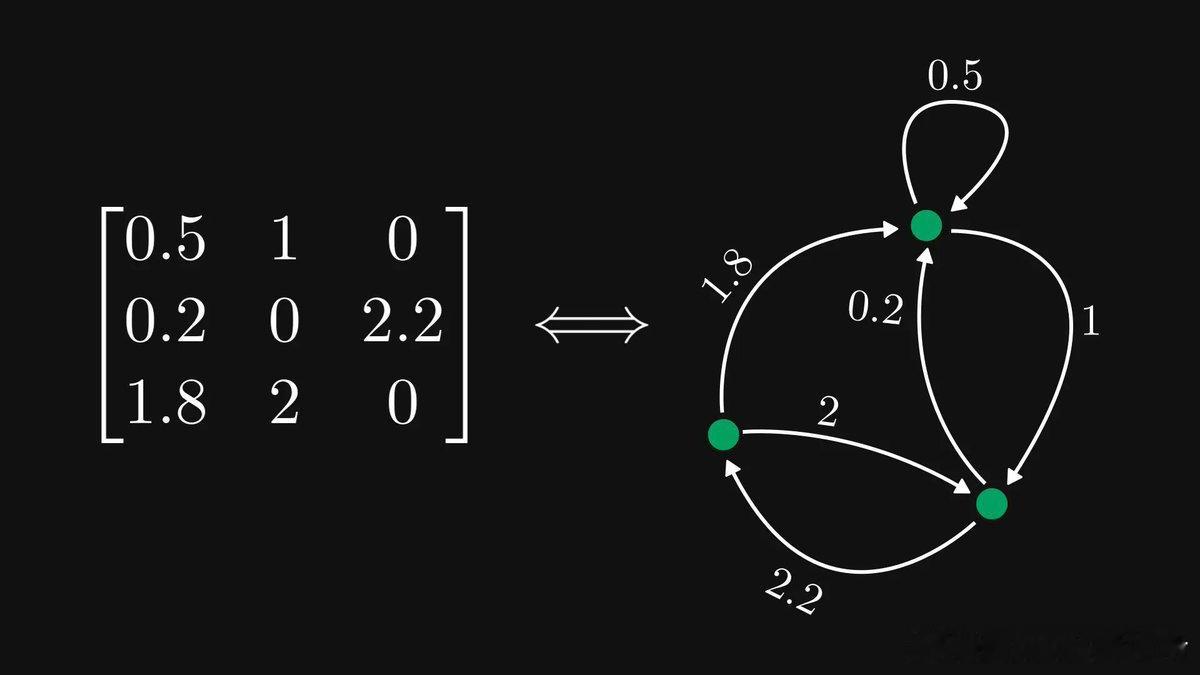
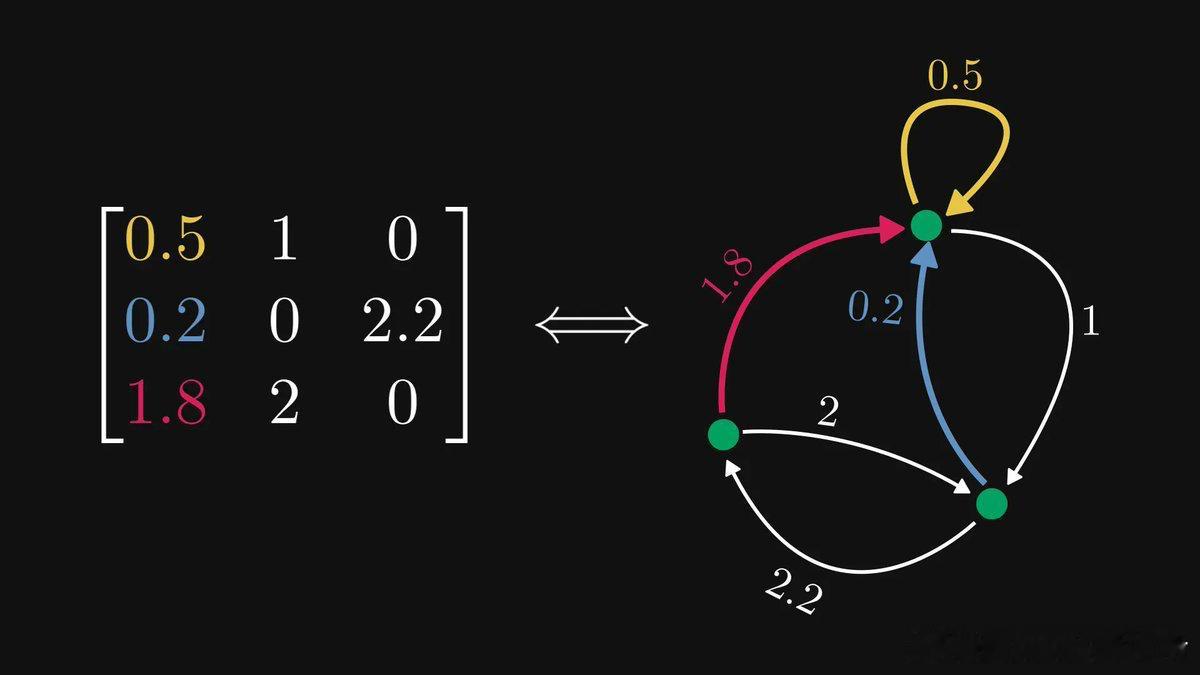
—— 每一行代表一个节点,每个元素代表有向加权边(零元素不画边)。第i行第j列的元素,就是从节点i指向节点j的边权。
举例说明:
- 矩阵的“行”对应出边,“列”对应入边。
- 矩阵的幂次(如A²)对应图中所有可能的多步路径。
- 若图是马尔可夫链状态转移图,矩阵幂次直接体现多步转移概率。
更深一层:
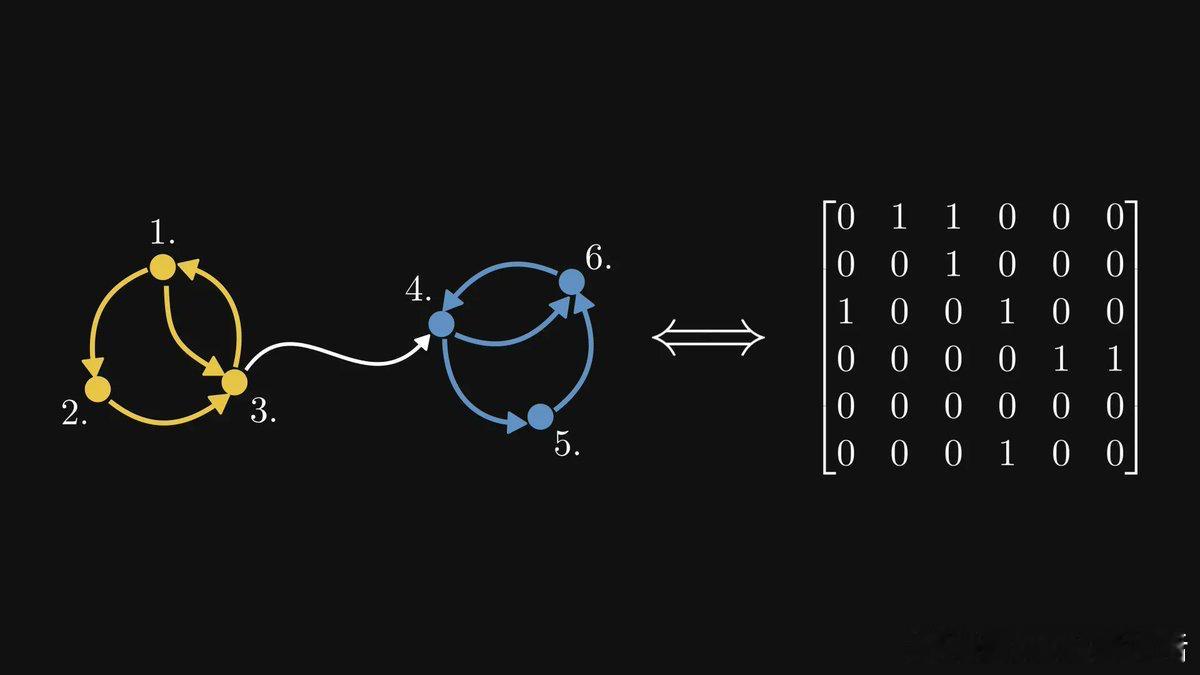
强连通分量(Strongly Connected Components)——图中每个节点都能互相抵达的子集,对应矩阵中的“不可约块”。
不可约矩阵 ↔ 强连通图;可约矩阵 ↔ 非强连通图。
通过图,我们能将任意非负矩阵化简为“Frobenius标准形”:
矩阵可划分为对角线上不可约块的块矩阵,且对角线下方块为零。
这个结构揭示了矩阵深层次的内在连接性和简化方式。
此外,矩阵与图的关系帮助我们定义图的特征值,使图论与线代相辅相成,开辟了新的研究视角。
总结一句我写的诗,表达发现这层联系时的感悟:
> “研究结构,剥去表象,直至骨骼显现。”
想深入掌握线性代数与机器学习的基础,而非盲目追新?
欢迎关注我的周报,已有3万+机器学习实践者加入:thepalindrome.org
---
原推文链接:x.com/TivadarDanka/status/1972360678100046072
---
【附加思考】
把矩阵视作图,不仅是数学上的“换个角度”,更是理解复杂系统、网络结构、动态过程的桥梁。
它让抽象的数值变成可视化的路径,让代数运算具备实际意义,有助于机器学习、信号处理、网络分析等领域挖掘本质。
这也提醒我们,数学语言的力量在于多样化的表达方式,掌握其中的转换,能极大拓宽解决问题的视野和效率。