求阴影部分面积方法合集✅掌握拿高分💯

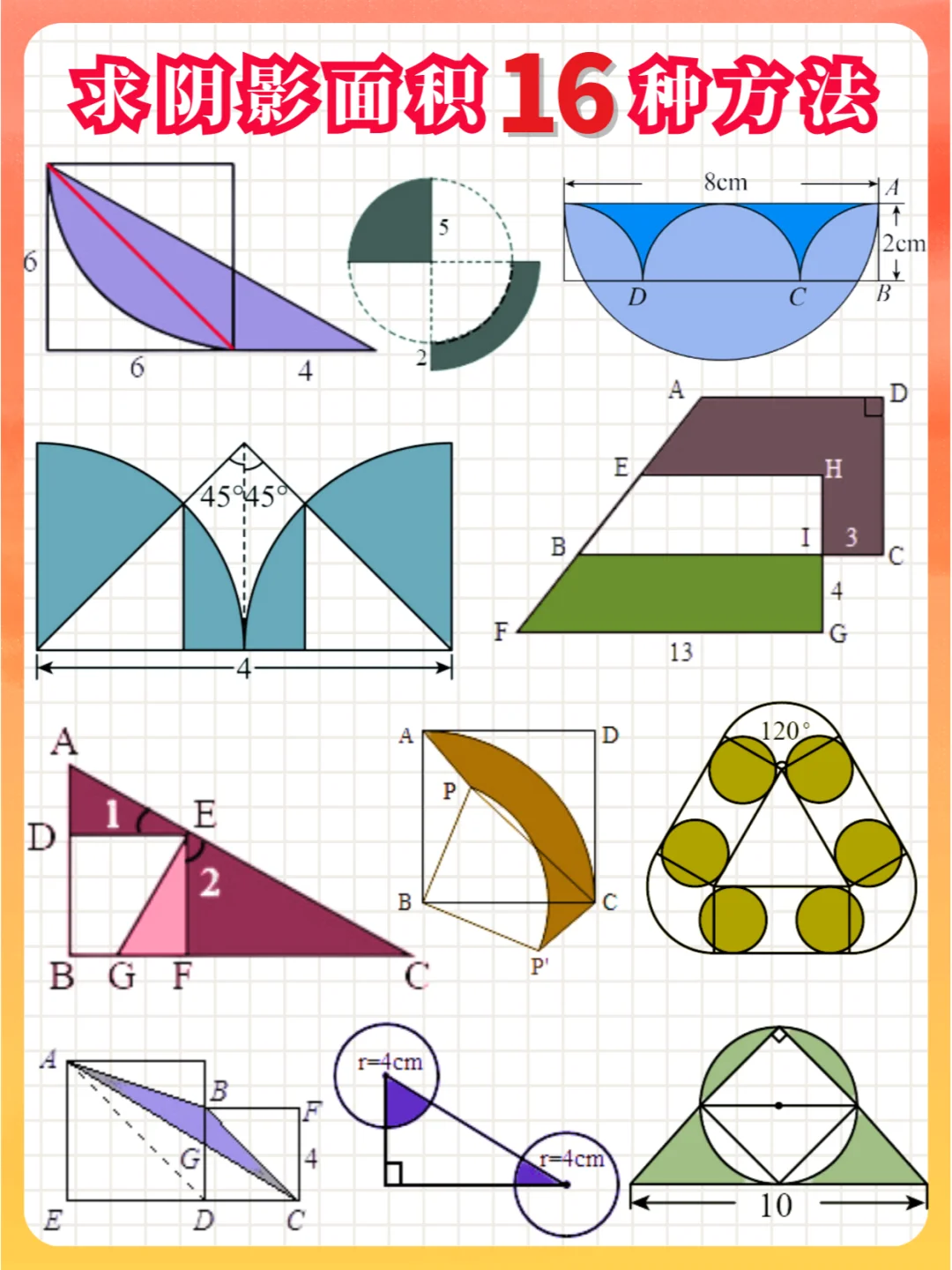
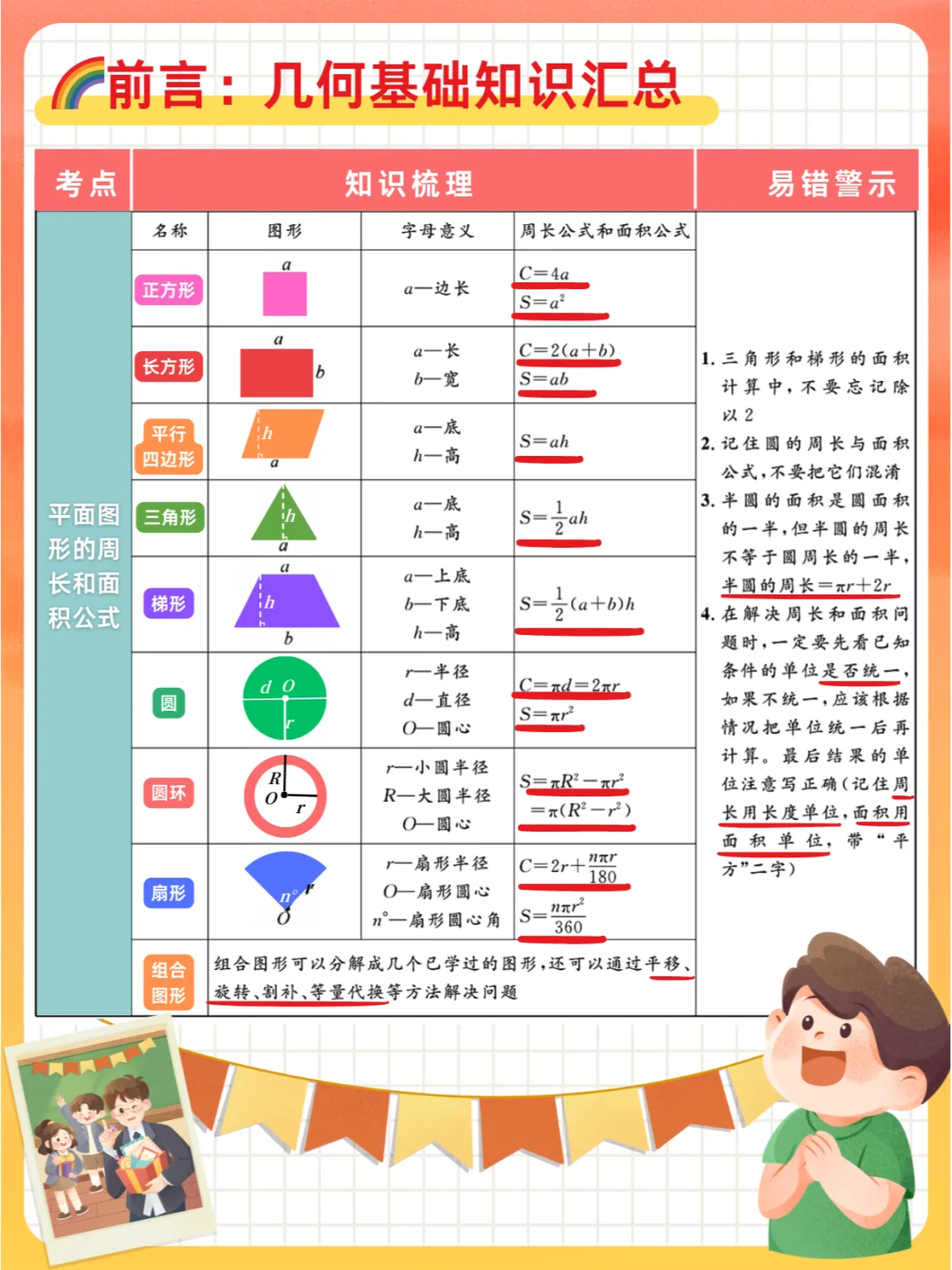
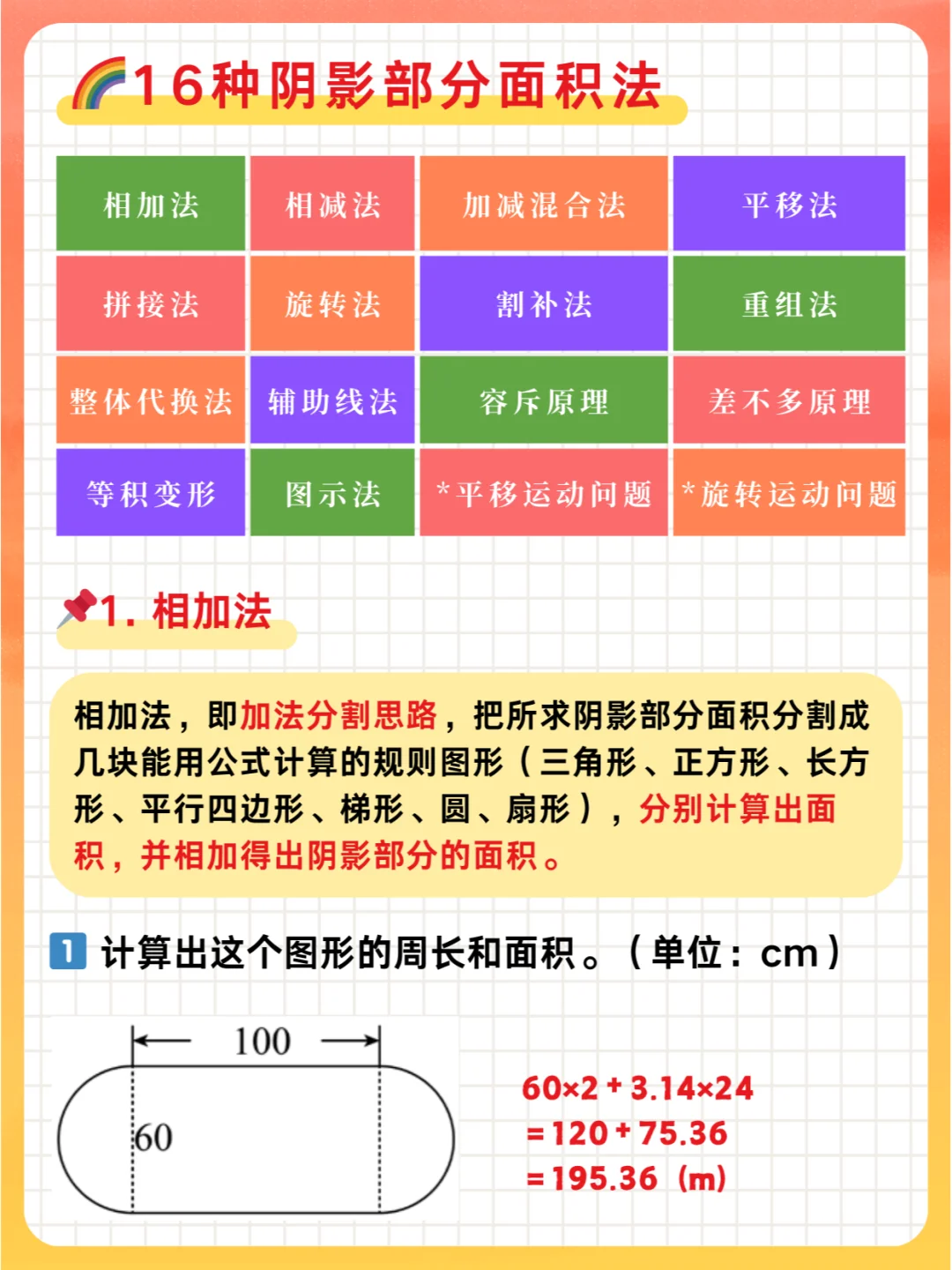
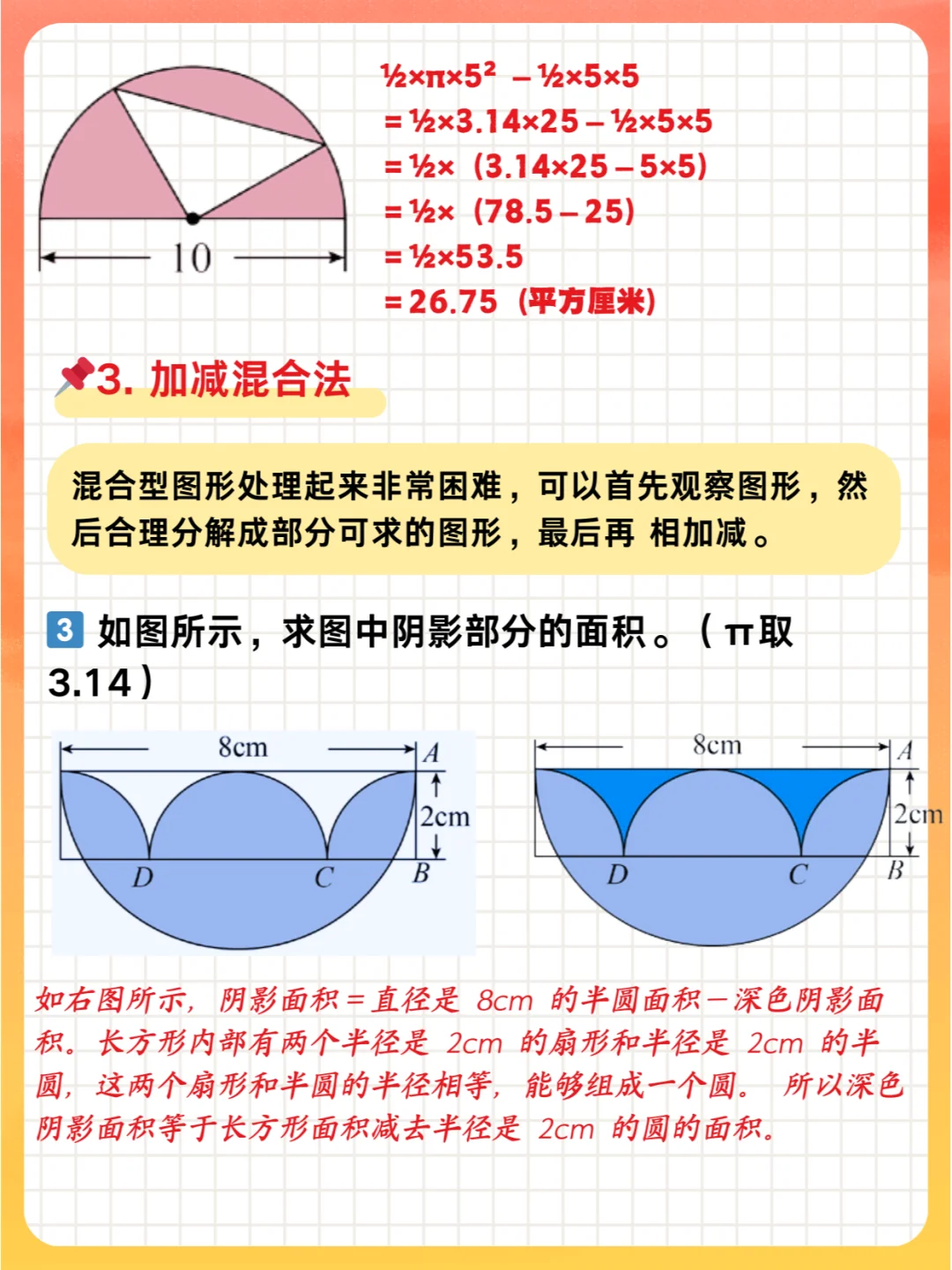
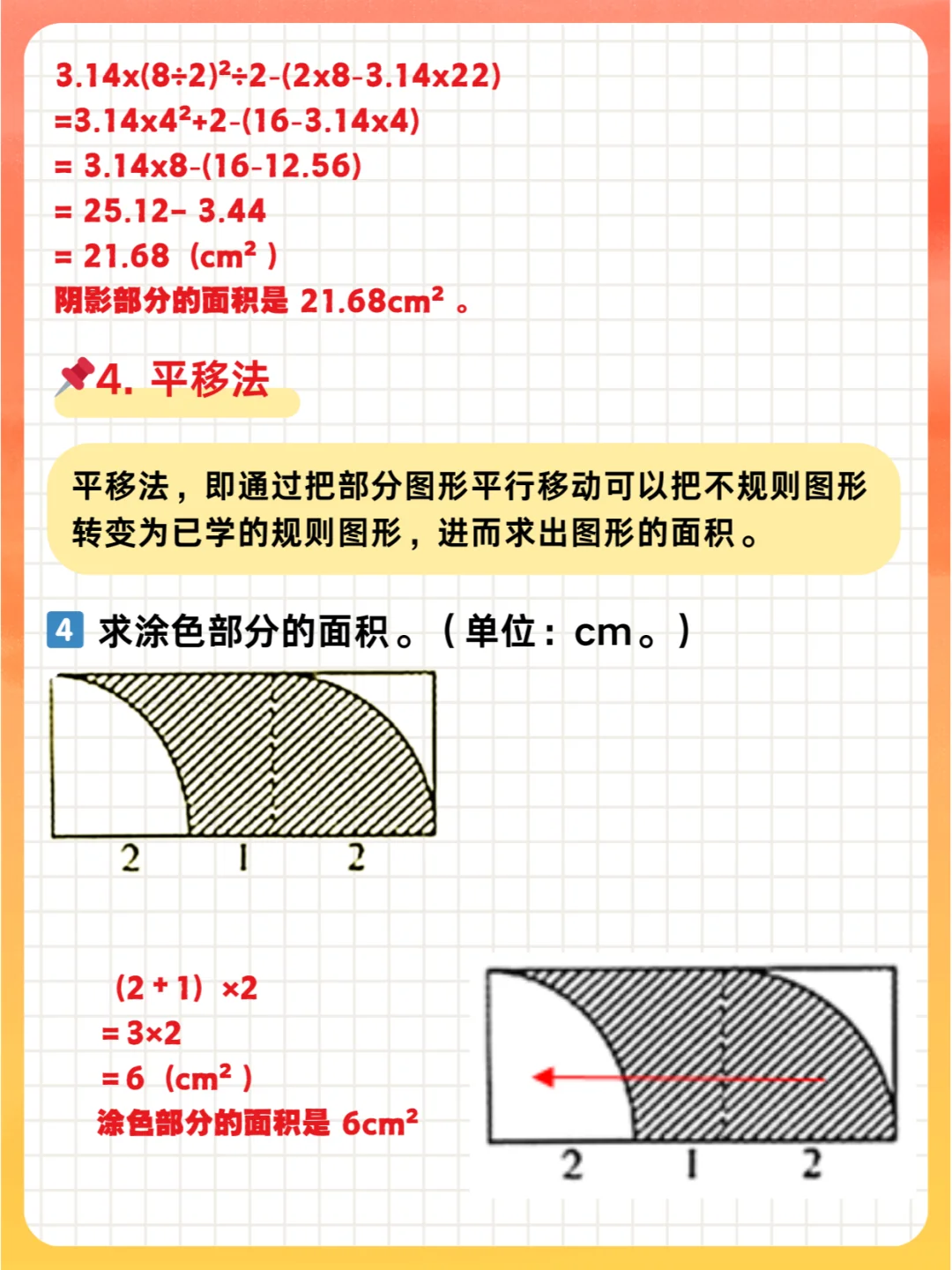
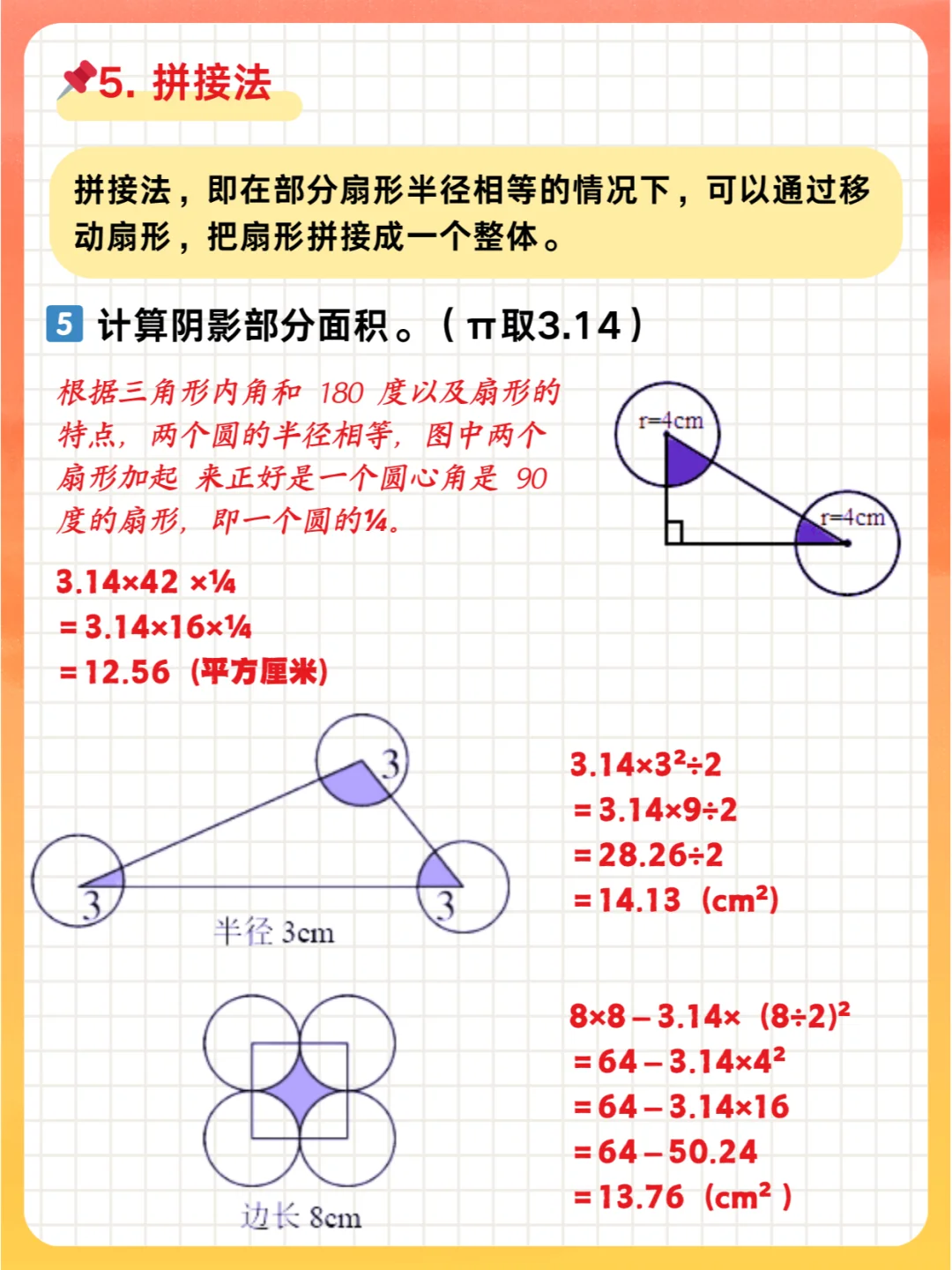
🌈六年级：小升初 几何 求阴影部分面积1️⃣6️⃣种解题方法大汇总，授人以鱼不如授人以渔，掌握方法，才能举一反三，避免无效刷题✅ 1️⃣相加法：即加法分割思路，把所求阴影部分面积分割成几块能用公式计算的规则图形，分别计算出面积，并相加得出阴影部分的面积。 2️⃣ 相减法：即减法拓展思路，是把不规则图形阴影部分面积拓展到包含阴影部分的规则图形中进行分析，通过计算这个规则图形的面积和规则图形中除阴影部分面积之外多余的面积，运用“总的”减去“部分的”方法解得答案。 3️⃣ 加减混合法 ：混合型图形处理起来非常困难，可以首先观察图形，然后合理分解成部分可求的图形，最后再相加减。 4️⃣ 平移法 ：即通过把部分图形平行移动可以把不规则图形转变为已学的规则图形，进而求出图形的面积。 5️⃣ 拼接法 ：即在部分扇形半径相等的情况下，可以通过移动扇形，把扇形拼接成一个整体。 6️⃣ 旋转法 ：又叫翻转法，即根据图形的特征，将原图的某一部分进行翻转或旋转，最后得到便于求 解的新图形。 7️⃣ 割补法 ：即分割拼补的思路，是把不规则的阴影面积通过分割和拼补，使之变为一个面积大小 不变且能实施计算成面积相同的规则图形。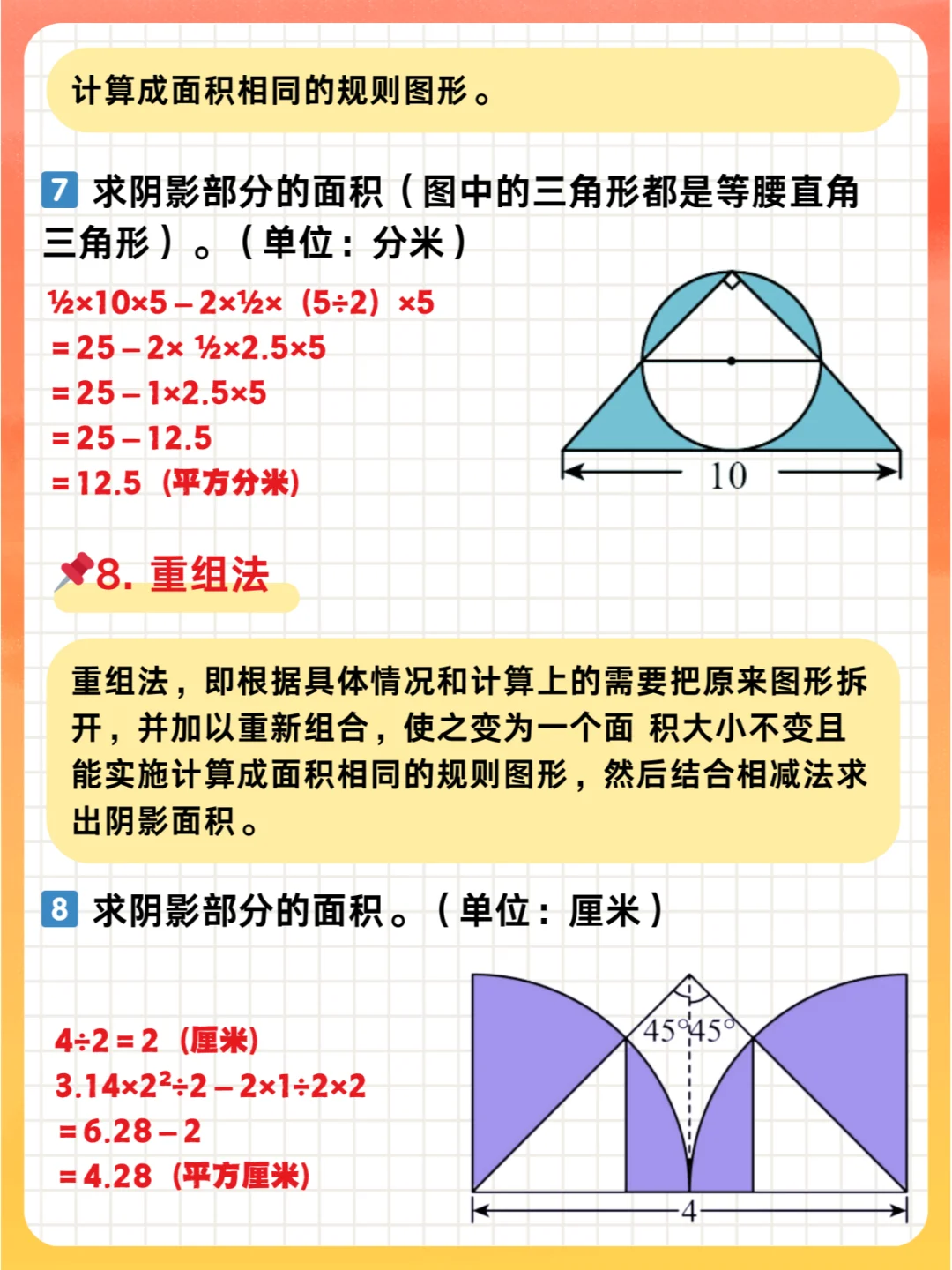 8️⃣ 重组法 ：即根据具体情况和计算上的需要把原来图形拆开，并加以重新组合，使之变为一个面 积大小不变且能实施计算成面积相同的规则图形，然后结合相减法求出阴影面积。 9️⃣ 整体代换法 ：即通过平面图形之间的等量关系，将图形面积整体代换，再根据相应面积公式求出面积。 🔟 辅助线法 ：即在通常手段无法求出阴影部分面积时，需要尝试使用添加辅助线的方法解决。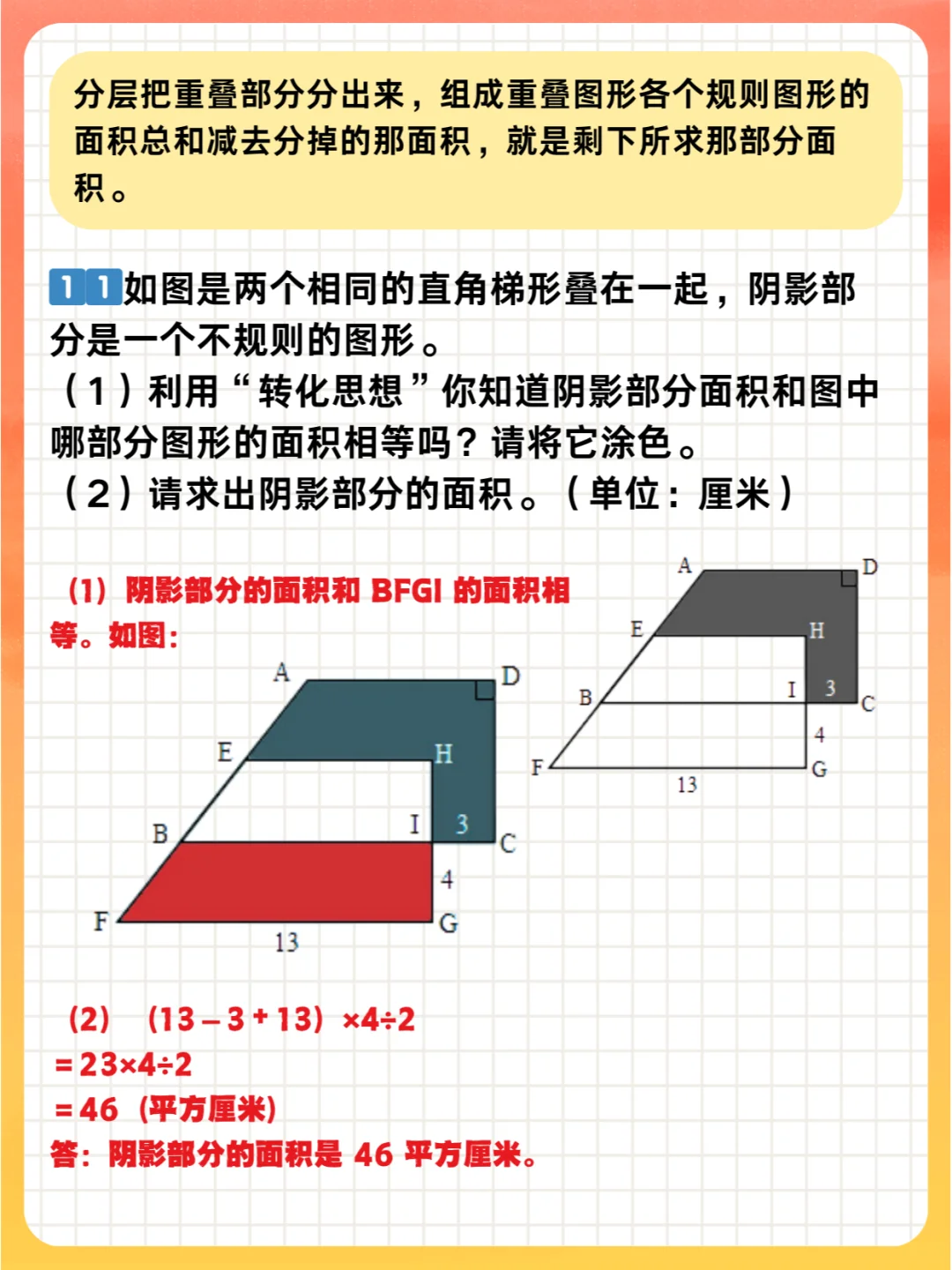 1️⃣ 1️⃣ 容斥原理 ：即重叠、分层思路，把图形中不规则的阴影部分看作几个规则图形用不同的方法重叠的结果，利用分层把重叠部分分出来，组成重叠图形各个规则图形的面积总和减去分掉的那面积，就是剩下所求那部分面积。 1️⃣ 2️⃣ 差不多原理 ：即利用等式的性质来求面积，如果 S 甲=S 乙，那么 S 甲+S 空白=S 乙+S 空白， 反之亦可。 1️⃣ 3️⃣ 等积变形 ：即利用等底等高，面积相等的特性，将不能求出的图形转化为面积与之相等的图形。 1️⃣ 4️⃣ 图示法 ：即先根据题意，画出图形的轨迹，再求面积。 ……